刷题笔记0x08:石子游戏
题目描述#

思路#
首先,我们要求的答案是两人中谁会赢,或者说最终谁手中的石子数多。
其次,我们知道两人都是高手,将发挥出最高水平,并且石子总数为奇数,一定会有人赢。
那么让我们假设f(i, j)为对于一个序列索引i到j区间内,先手玩家最大所得与后手玩家最大所得的差值。
先假设个数组piles为[2, 7, 3, 9]的例子画个图看看。
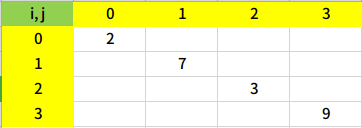
先不急着把所有情况填满,显而易见的是,对于i = j的情况,差值显然就等于piles[i]或者说piles[j]了(因为这种情况区间里就一堆石头啊,后手根本没得拿)。
另外还可以发现,类似i = 1, j = 3和i = 3, j = 1的情况,它们表示的是同样的区间,所以我们可以抛弃表格左下角,并假定0 <= i <= size && i <= j <= size,其中size表示题目给定的数组长度。
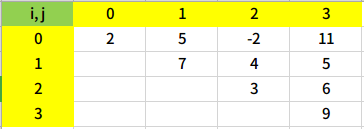
但是这样好像不太好总结规律,让我们稍微调整一下表格,每个表格里放两个数,分别表示先手可得的石子数和后手可得的石子数。
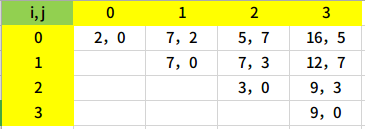
对于先手而言,只有两种选择,拿左边的或者右边的,我们设置一个三维数组dp[i][j][2],dp[i][j][0]表示先手在区间内可得石子数,dp[i][j][1]就是后手的了。
dp[i][j][0] = max(piles[i] + dp[i-1][j][1], piles[j] + dp[i][j-1][1]);
/*
当我是先手时,比如说我拿走最右边一堆piles[j],
那么当前情况,相当于是对方是先手(dp[i][j-1][0])
而我变成dp[i][j-1]情况下的后手
拿左边同理
*/
// 先手拿了左边时,后手是[i-1][j]情况下的先手
dp[i][j][1] = dp[i-1][j][0];
// 同理先手拿走右边时
dp[i][j][1] = dp[i][j-1][0];
// 再回到我们最开始发现的规律
// if i == j: 先手拿走唯一的那堆石头
dp[i][j][0] = piles[i];
dp[i][j][1] = 0;代码实现#
具体写代码时,我们要得到的答案就是表格的右上角dp[i][j][0] > dp[i][j][1]这个表达式是否为true,也就是先手是不是比后手拿的石头多。为此,我们可以试着斜着遍历数组直到右上角。
bool stoneGame(int* piles, int pilesSize)
{
int dp[pilesSize][pilesSize][2];
memset(dp, 0, sizeof(dp));
// 基准情况
for (int i = 0; i < pilesSize; i++)
{
dp[i][i][0] = piles[i];
dp[i][i][1] = 0;
}
// 斜着遍历数组
for (int l = 2; l <= pilesSize; l++)
{
for (int i = 0; i <= pilesSize - l; i++)
{
int j = l + i - 1;
int left = piles[i] + dp[i+1][j][1];
int right = piles[j] + dp[i][j-1][1];
// 省去写一个max函数
if (left > right)
{
dp[i][j][0] = left;
dp[i][j][1] = dp[i+1][j][0];
}
else
{
dp[i][j][0] = right;
dp[i][j][1] = dp[i][j-1][0];
}
}
}
return dp[0][pilesSize-1][0] > dp[0][pilesSize-1][1];
}后记#
这道题的条件我隐约觉得有些不对劲,翻了一下评论,果然,这个游戏居然先手必胜,也就是说这题有个时间复杂度为O(1)的解法:
return true;
