刷题笔记0x07:不同路径
不同路径#
描述#
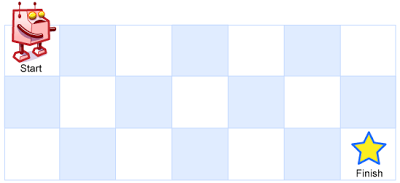
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。 问总共有多少条不同的路径?
思路#
首先想到的是,既然这个机器人只能向下或向右走,那么,设机器人当前所在位置坐标为(x, y),可以得出结论,机器人只能从(x-1, y)或(x, y-1)来。
现在,让我们设函数f(x, y)为机器人到达坐标点(x, y)的路径数。那么,由之前的结论可得出公式,即f(x, y) = f(x-1, y) + f(x, y-1)。
另外,对于所有合法的终点(也就是除了起点以外),当y = 0或x = 0时,路径数都为1。
代码#
在具体实现时要考虑一下,如果用二维数组来记录从起点到终点的路径数,C语言数组的索引是不能为负数的。例如有一个3 x 2的格子,可以如下表操作:
| 0 | 0 | 0 | 0 |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
将3 x 2的格子改造成4 x 3,并且外圈置0,同时把坐标为(1, 2)的格子与(2, 1)的格子置为1,因为从起点到这两点路径数都为1,这样后面所有坐标都有了计算的基点。对于这一点如果不能理解,可以在纸上画图,并把后面坐标的值按照公式f(x, y) = f(x-1, y) + f(x, y-1)填一下。
这样,我们相当于把原本的格子向右下移动了,以此避免索引出现负数。
首要工作就是要声明数组并赋值:
int dp[m+1][n+1];
// 全部置0
memset(dp, 0, sizeof(dp));
// 先把这两个坐标设为1
dp[1][2] = 1;
dp[2][1] = 1;接着就可以迭代计算了,既然我们把格子向右下移动了,那么要从索引1开始。
for (int x = 1; x <= m; x++)
{
for (int y = 1; y <= n; y++)
{
// 前面我们已经设好这两个坐标的值为1了,不能把它们又改掉了
if ((x == 1 && y == 2) || (x == 2 && y == 1))
{
continue;
}
dp[x][y] = dp[x-1][y] + dp[x][y-1];
}
}完整代码如下,之所以要先有个if判断,是因为这个题目输入1,1时要返回1:
int uniquePaths(int m, int n)
{
if (m == 1 || n == 1)
{
return 1;
}
int dp[m+1][n+1];
memset(dp, 0, sizeof(dp));
dp[1][2] = 1;
dp[2][1] = 1;
for (int x = 1; x <= m; x++)
{
for (int y = 1; y <= n; y++)
{
if ((x == 1 && y == 2) || (x == 2 && y == 1))
{
continue;
}
dp[x][y] = dp[x-1][y] + dp[x][y-1];
}
}
return dp[m][n];
}
排列组合#
这一题其实还可以用高中数学方法解决,因为这其实就是个排列组合问题。这个留给读者自己去想啦。